ミクロ経済学を学ぶときに最初のほうに出てくる「予算線」。

いきなり難しい話になりそうな雲行きだが、実際にお話しするのはすごくシンプルな原理。ちょっとだけ辛抱して読んでもらえればと思います。

※最初に言い訳をするんだけど、ふつうはミクロ経済学を学ぶときには無差別曲線というのを同時に学ぶと思う。しかし、今回は無差別曲線まで入れるとめっちゃ長くなっちゃうし、要点は予算線だけでなんとか説明できるので、無差別曲線には触れません。いつか無差別曲線も混ぜて短く論じることができるようにがんばります。

予算線をいう概念を使って、商売人の永遠の命題である「いいものを作ればきっと売れるはずだ（品質が良ければ売れる）」と、それから「一生懸命やればきっと売れるはずだ（サービスが良ければ売れる）」が条件によっては正しくない（つまり売れない）ことを考察する。

このふたつを対立する二つの項目とする理由は、同じ売価（とコスト）で品質もサービスも両方を上げることはできないため、経営者の好みでどっちかに注力しがちである、ということからである。

予算線とは何か

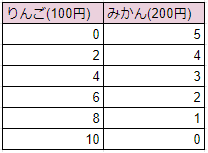
予算線というのはミクロ経済学だと簡単な例として「りんごが100円、みかんが200円のときに、予算1000円でめいっぱい買うことのできる範囲」というような形で紹介される。有り金はたいて1000円という制約があるので、りんごを5個、みかんを3個買うことはできないので、予算制約線と言うこともある。

で、これは非常に簡単な方程式を解くことでパッとわかる問題であり、組み合わせで言えば次の表のようになる。

方程式としては、りんごをR、りんごの個数をx、みかんをＭ、みかんの個数をyとして、所持金を￥とすると、

￥=Rx+My　(1)

となる。ので、

1000=R*0+M5　から　R*10+M0　まで

Rは二個刻みで、Ｍは一個刻みでそれぞれ増加と減少をさせた組み合わせを取ることになる。

ここまではいいでしょうか。

さてこれをグラフに描くとこうなる。

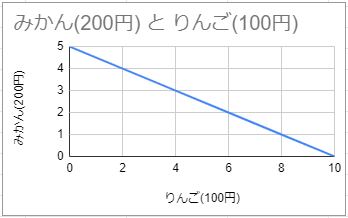
こういう、右下がりのグラフになる。

例えば、みかんを2個とりんごを2個、というような買いかたもできるのだけど、この場合、予算を使い切るようにグラフが描かれている（という前提になってる）ので、みかん2個とりんご2個という組み合わせでは買わないとする。

このグラフは(1)を満たすのは明らかなので（というか(1)の式からグラフを描いているので）、この直線上のすべての点で1000円を使い切ることができる。

このグラフが予算線である。りんごやみかん、所持金などをいろいろ読みかえることで、いろいろなことがわかる便利なグラフである。

予算線を使ってカフェにおける品質とサービスの組み合わせを考えてみる

予算線（予算制約線）が何なのかがわかったところで、実際にこれを使って、冒頭にある「いいものを作ればきっと売れるはずだ（品質が良ければ売れる）」と、それから「一生懸命やればきっと売れるはずだ（サービスが良ければ売れる）」が正しいのかどうか、条件によっては正しくない（売れない）という可能性があり、商売人はよくその罠にはまってしまうという現象を説明していこう。

予算線は、その名の通り「おいくらの予算でお買い物をなさいますか」という話なので、1000円を持っている消費者の立場で品質とサービスについて考えてみる。

それでは読者の皆さんも1000円を持ってカフェに行ってみたと思って、ここから下を読んでみて欲しい。

所持金を￥、品質をＱ、品質の値段（というものは単位があるわけではないがこの場合100円刻みで価値を感じるとする）をx、サービスをS、サービスの値段も同じ理由をあてはめつつyとすると、方程式は

￥=Qx+Sy　(2)

となる。

品質やサービスと言っても漠然としているので、それぞれの要素となりそうなものを書き出してみる。

品質（原材料が良い、製造工程が良い、原産地が有名だったり希少だったり、HACCPやISOの取得などなど）

サービス（利便性が良い、好立地、スタッフの対応、店舗の雰囲気、安価などなど）

その組み合わせは以下の表のようになる。

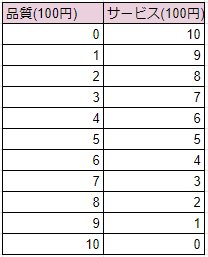
そしてこの表をグラフに描くとこうなる。

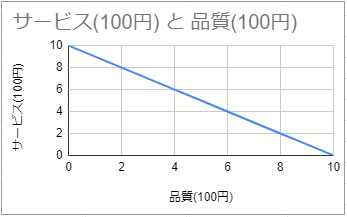
さてこのグラフから、消費者はカフェで1000円を使うときにこの右下がりの直線上のどこの点で消費してもいい、ということがわかる。なぜなら、そのときの消費額は変わらないからだ。

それでは、カフェはこの直線上のどこに品質とサービスのバランス点を置けばいいのか。いいのかと聞いておいてなんだがそれはカフェの自由なのである。特にどこでなければいけないということはない(*1)。品質10でサービス0でいくぜ！、というお店もあれば、品質もサービスも同じくらい重視、というお店もあるだろう。この直線上のどの組み合わせであっても、お客さんが1000円を支払うことにかわりはないので、どのへんを重視するかはお店の戦略による。

サービスが良ければお客さんは勝手に来るのか

お客さんからしてみたら、1000円をそのお店に支払うことでなにがしかのリターンが欲しいということだ。

お店からしたら、サービスは悪いより良いほうが断然お客さんにはメリットがあるわけだから、サービスをすごく良くすればきっとお客さんは喜んで1000円を支払ってくれるだろうと考える。・・・というのはまあ道理だと思っちゃうけど、実はそうはなりにくいぞ、ということを考えてみたい。

時間が経てば良いサービスも陳腐化し同じお金で受けられるサービスは低下する

前提として、時間が経てば「世の中は進歩する」「お金の価値は下がる（インフレ傾向である）」とする。これは納得感があるのではないだろうか。世の中は便利になり新しいものが市場に出回り生活は豊かになる。そして昭和の昔にアルトは48万円だったが（わかる人の少ない例えですんません）いまやアルトは100万円前後もするのだ。

さて、そうするとどうなるか。良いサービスも陳腐化し、同じサービスであれば必要なお金はどんどん増えていくわけである。

それを表にしたらこうなる。

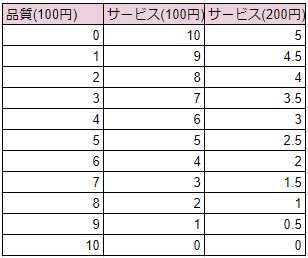
左の列は品質であるが、品質は100円単位のままである（サービスがゼロの場合は10単位で1000円になる）。真ん中の列は、ある時点のサービスを表すが、これは100円が10単位であり、品質がゼロの場合には10単位で1000円が最大になる。そして右の列であるが、これは時間が経過した後のサービスを表す。お金の価値が下がったため、真ん中の列のサービスと同じサービスであれば200円かかるとなり、最大は5単位で1000円となる。

これをグラフにするとこのようになる。

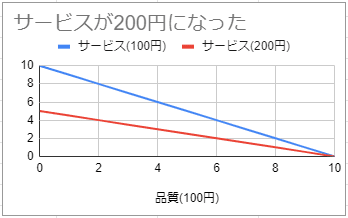
この青い線が、品質と、ある時点でのサービス（100円が1単位）の組み合わせであり、赤い線は、品質と、時間が経過した後のサービス（200円が1単位）の線である。

この図からわかるのは、サービスに全振りすると顧客の満足度の低下が激しくなるということである。

お客さんにしてみれば「前は1000円でこのくらいのサービスが受けられたのに、今では品質は変わらないのにサービスが低下して、それで金額は同じ1000円か」となるわけである。

注意してもらいたいのは、時間が経過しても品質は同じ100円で10単位ということになっているところである。これは、なぜサービスと同じように時間の経過によって200円の5単位にならないかというと、お店がサービスに全振りしている場合、品質に対する期待値はゼロなので、もともとゼロであるところに2分の1をかけてもゼロだからである。言い換えれば、サービス全振りのお店に来るお客さんはそもそも品質を気にしていないので、時間の経過によって品質が陳腐化しその価値が下がったとしても、1000円の中に品質の割合が無いわけだから、まったく関係が無いわけである。

このような理由により「一生懸命まじめにやってるのに」お客さんは来なくなる。

もちろん、このサービスと品質を入れ替えれば品質に全振りしたお店の場合となり、同じ理由により「一生懸命良いものを提供しているのに」お客さんは来なくなる。

なお、グラフを読むと、サービスに全振り（品質に全振りも同じ）した場合にその価値が半減するとそのまま顧客の満足度は半減するが、サービスと品質をちょうど半分ずつの価値だと思っているお客さんの場合には、横軸の目盛りで5のところになるため、顧客満足度は25％しか下がらない(*2)。これはサービス全振りと品質全振りのグラフを重ね合わせるとその交点から読み取ることができる。

しかし、必ず5対5の割合を目指さなければならぬ、ということでもないと思う。それは、実際に経営をする場合にはほかにもたくさんの要素が混じってくるからである。しかしながら、一定の予算の中で消費をするお客さんを長いあいだつかまえるには、二つの項目を同時にある程度ずつ満たす必要があるというのはわかっていただけたかと思う。

お客さんのニーズに応えるのはたいへん

お客さんは様々なニーズを持っている。そのニーズを大きく「品質」「サービス」と二つのラベルに分けて、そしてその組み合わせについて考えた。結局はどっちかに全振りするのは顧客満足度が下がるよ、という話をしたわけだけど、この2項目の組み合わせに対する分析は細かくしていくこともできるので、例えば「いまスタッフ不足だけど、営業時間を短くするかそれともスタッフを増員するか」「ランチタイムとカフェタイムでメニューを増やすならどっちかな」とか「改装をしたいんだけど、シックな感じにするかポップな感じにするか悩む」とか、いろんなものを考えてみるといいと思う。どのくらいの割合でどっちに注力しようかな、というひとつの目安になるかと思うし、極端にどっちかに振るリスクを理解しやすいかと思う(*3)。

*1 無差別曲線を同じ平面上に描ける場合には、最適消費点、つまり消費者がどの組み合わせで購入するのがもっとも効用が高くなるかが決定されるのだが、それはまた別の話で

*2 グラフを省略するのは、うまくエクセルでグラフを描くことができなかったためですすんまそん

*3 それでも個性バリバリのめっちゃ偏った志向にするぜ、というのも突き抜けて一つの最適解かなとも思う。それは、利益を増やすためにリスクを取るという行動は経済学的にも説明がつくからであるが、それはまた別の話で